15 August 2018

Looking at randomness and performance for hash codes

In these articles, String.hashCode() is not even a little unique and Why do I this String.hashCode() is poor, I looked at how String.hashCode() might have been made better with little change at the time it was last updated (in Java 1.2). However, given the current solution has been in place for 20 years, the default behaviour is unlikely to change. Additionally, if we were to consider different a different algorithm I would prefer something much faster and more random than just changing the prime factor from 31 to 109.

How can we evaluate randomness?

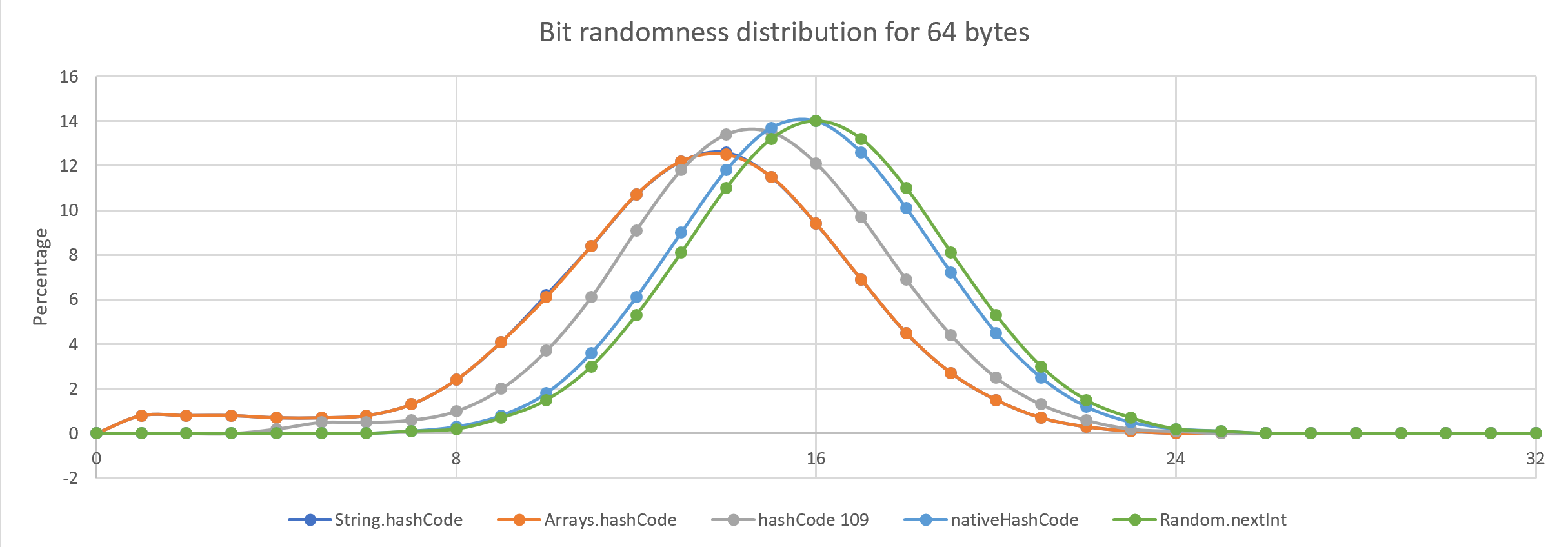
One way of looking at randomness is to change the input by one bit and see how many bits change in the resulting hash. The input is first populated with random data and the resulting hashes are compared for a large sample. In this case, I took one million samples and plotted it against what you get for a Random.nextInt() call.

The ideal hash changes half of the bits on average, more than half bits changed is also a bias.

Figure 1. The randomness of the hash code for different strategies for longer inputs compared with Random all have decent outcomes

Harness to estimate the randomness distribution of a hashing strategy.

static double[] randomnessDistribution(ToIntFunction<byte[]> hashCode, int length) {
    double[] dist = new double[33];
    Random random = new Random(length);
    byte[] bytes = new byte[length];
    int tests = 0;
    for (int t = 0; t < 1000000; t += length) {
        for (int i = 0; i < length; i++)
            bytes[i] = (byte) (' ' + random.nextInt(96)); (1)
        int base = hashCode.applyAsInt(bytes);

        for (int i = 0; i < length; i++) {
            for (int j = 0; j < 8; j++) {
                bytes[i] ^= 1 << j;
                int val = hashCode.applyAsInt(bytes);
                int score2 = Integer.bitCount(base ^ val);
                dist[score2]++;
                tests++;
                bytes[i] ^= 1 << j;
            }
        }
    }
    for (int i = 0; i < dist.length; i++)
        dist[i] = Math.round(1000.0 * dist[i] / tests) / 10.0;
    return dist;
}

1	I assume the input is largely ASCII or positive bytes. This doesn’t change the results greatly.

Print the distribution of different strategies for charting.

for(double[] dist: new double[][] {
        randomnessDistribution(HashCodeBenchmarkMain::hashCode31, length),
        randomnessDistribution(Arrays::hashCode, length),
        randomnessDistribution(HashCodeBenchmarkMain::hashCode109, length),
        randomnessDistribution(HashCodeBenchmarkMain::nativeHashCode, length),
        randomnessDistribution(value -> ThreadLocalRandom.current().nextInt(), length)}) {
    System.out.println(Arrays.toString(dist).replaceAll("(\\[|\\])", ""));
}

Modified form of the String.hashCode() using 109 as a prime.

static int hashCode109(byte[] value) {
    if (value.length == 0) return 0;
    int h = value[0]; (1)
    for (int i = 1; i < value.length; i++) {
        h = h * 109 + value[i];
    }
    h *= 109; (2)
    return h;
}

1	On the first iteration don’t need to multiply the previous value.
2	Afterwards, multiply by the factor to improve the outcomes for short inputs.

The differences between hashing strategies are more obvious for shorter inputs.

Figure 2. Most strategies tested do well for 20-byte inputs

Figure 3. For 8-byte inputs, some strategies are not ideal

Figure 4. For 4 byte inputs, String.hashCode() and Arrays.hashCode() are poor

Figure 5. For 2 byte inputs, String.hashCode() and Arrays.hashCode() are not great

Figure 6. For 1 byte inputs, String.hashCode() and Arrays.hashCode() might be fine as the number of possible keys is small.

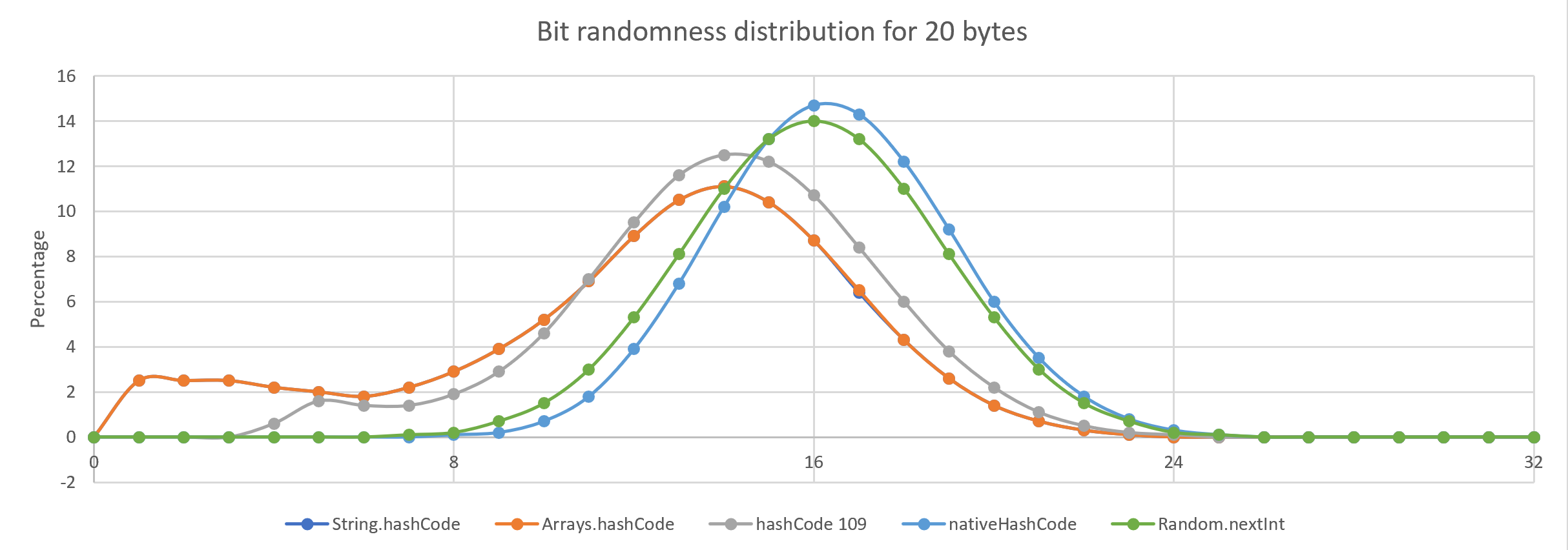
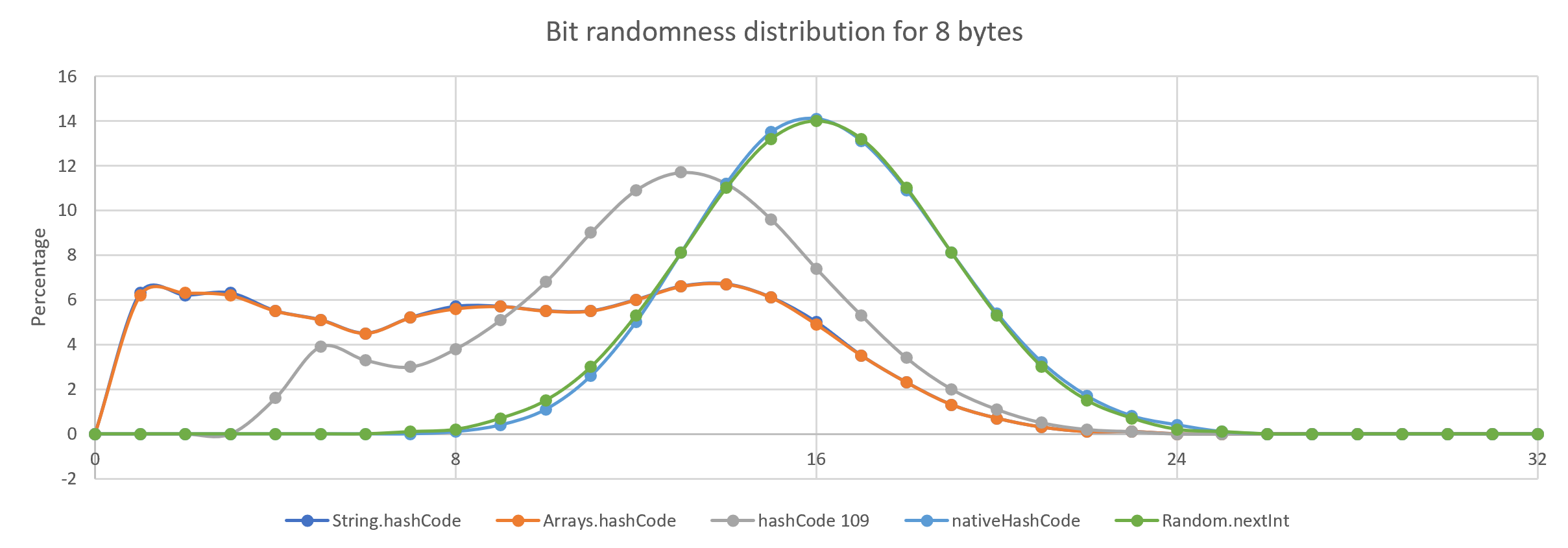
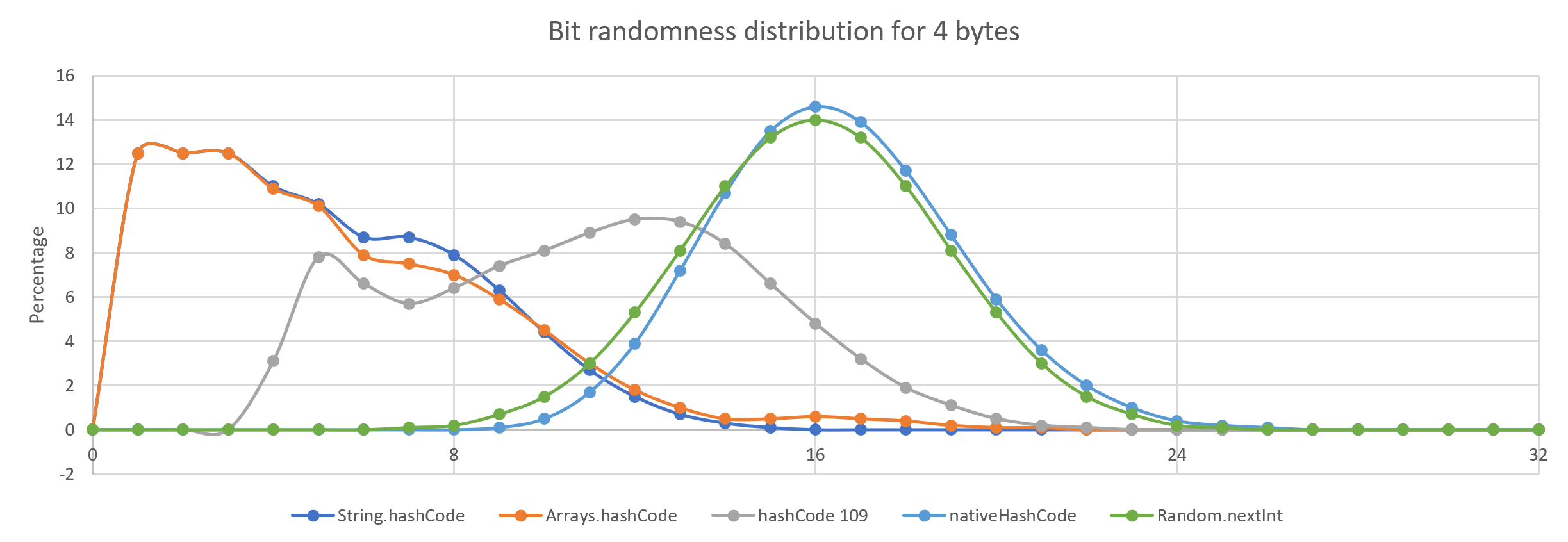
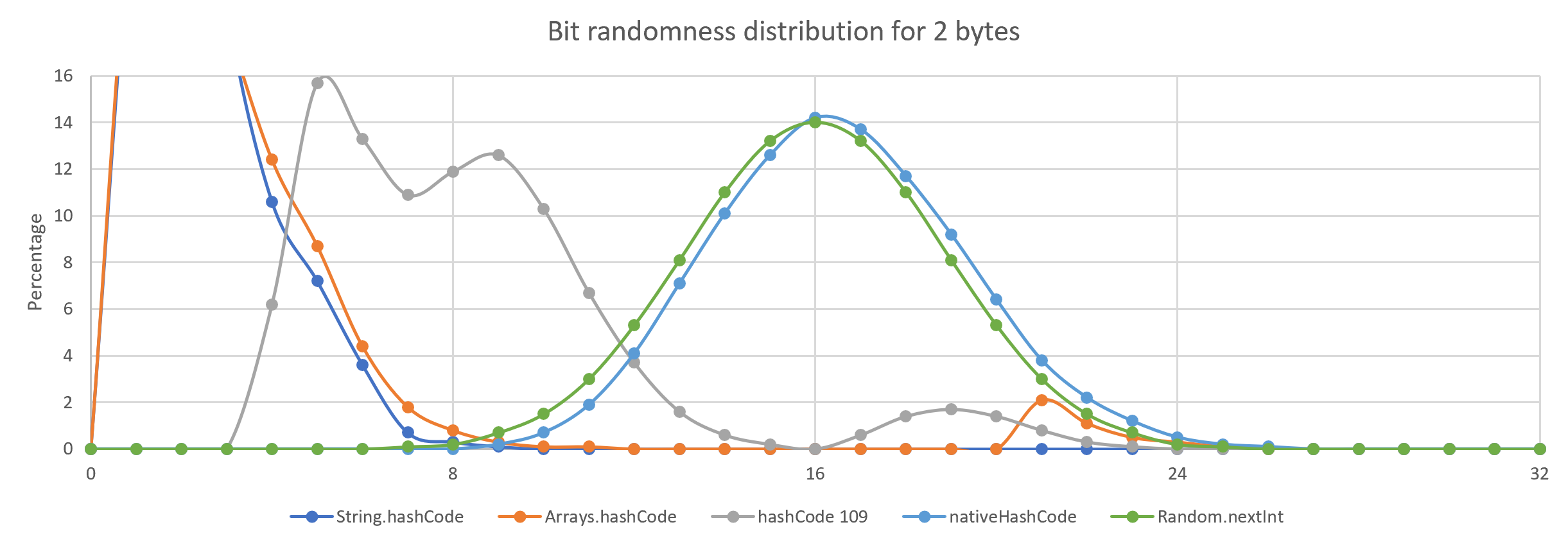
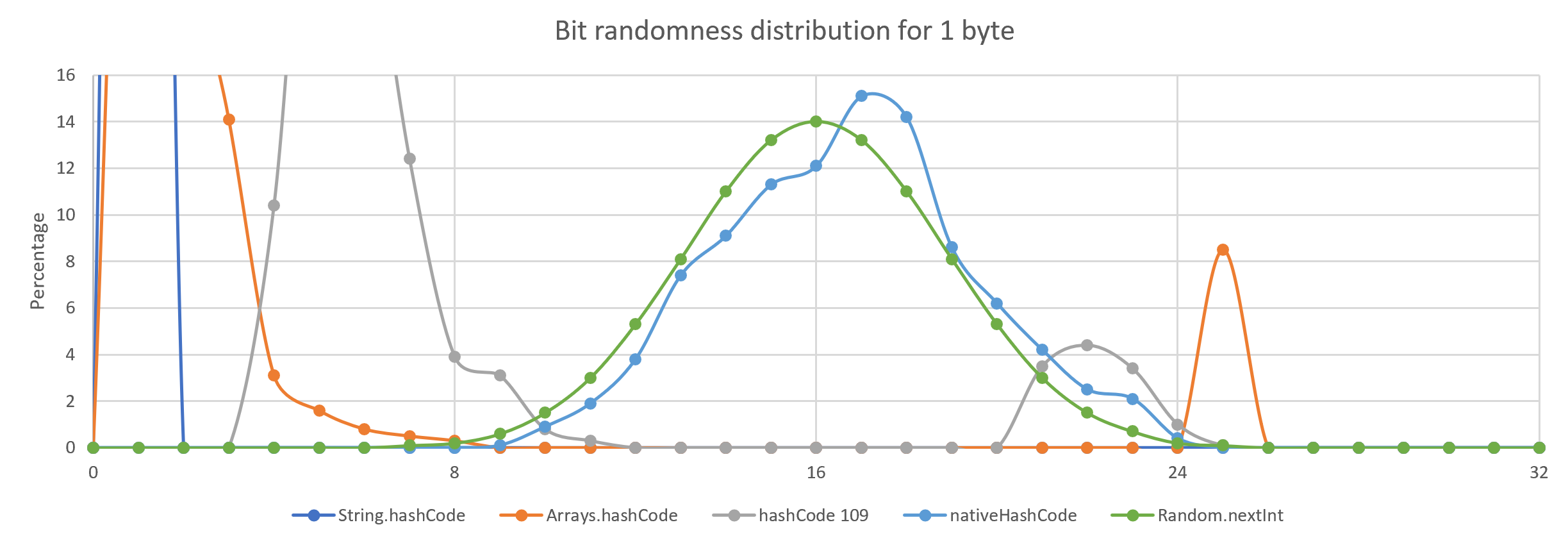
What is this "native" hashCode?

A technique we use to speed up the processing of bytes is to attempt to process groups of them at once i.e. 4 bytes or 8 bytes at a time. This can speed up processing by 2-4x. We also see a benefit in using a larger prime as we pass through fewer iterations.

Hashing strategy which takes 4 bytes aa time

private static final int M2 = 0x7A646E4D;

// read 4 bytes at a time from a byte[] assuming Java 9+ Compact Strings
private static int getIntFromArray(byte[] value, int i) {
    return UnsafeMemory.INSTANCE.UNSAFE.getInt(value, BYTE_ARRAY_OFFSET + i); (0)
}

public static int nativeHashCode(byte[] value) {
    long h = getIntFromArray(value, 0);
    for (int i = 4; i < value.length; i += 4)
        h = h * M2 + getIntFromArray(value, i); (1)
    h *= M2;
    return (int) h ^ (int) (h >>> 25);
}

1	assess assumes all byte[] have zero byte padding at the end and aligned to a multiple of 4 bytes.
2	in each iteration multiply by a large constant
3	agitate the results using some of the high bits

How can we measure how they perform?

Using JMH, we can benchmark how long each operation takes on average. To have reasonable coverage, the benchmark tried a number of sizes so this is the average for those sizes.

Benchmark comparing the throughput of using String.hashCode with 31 or 109 and the native hashing strategy.

Benchmark                                      Mode  Cnt   Score   Error   Units
HashCodeBenchmarkMain.String_hashCode         thrpt   25  15.586 ± 0.433  ops/us
HashCodeBenchmarkMain.String_hashCode109      thrpt   25  13.480 ± 0.147  ops/us
HashCodeBenchmarkMain.String_hashCode31       thrpt   25  16.173 ± 0.205  ops/us
HashCodeBenchmarkMain.String_native_hashCode  thrpt   25  55.547 ± 2.051  ops/us

The native implementation is around 3-4 times as it processes up to 4 bytes at a time.

The code

A maven module of code exploring how String is hashed is HERE

Conclusion

I believe it is possible to produce a hashing strategy which is both much faster and has a better hash distribution than the 20-year-old solution. Changing the JVM is impractical however having a pluggable hashing strategy for XxxxHashMap might ensure backward compatibility while providing an option for a faster solution.